Flexion
Lorsque une poutre est déformée par une force, alors il apparait des contraintes dans le matériau.1 - La contrainte de flexion

La définition de la contrainte (σ) :

![]()
Mf : Moment de flexion (N.mm)
I : Moment d'inertie (mm4)
v : position de la fibre la plus éloignée de l'axe neutre (mm)
Moments d'inertie :

La contrainte maxi doit rester inférieure à la résistance élastique Re, divisé par un coefficient de sécurité (s).2 - La condition de résistance
![]()
Une poutre soumis à un moment de flexion va se déformer de manière caractéristique, en fonction : On appelle flèche f la valeur de la déformation maxi3 - Déformée de la poutre en flexion
1) de la valeur et de la position de(s) la force(s)
2) de la nature des appuis
3) de la nature des liaisons avec reste de la structure.
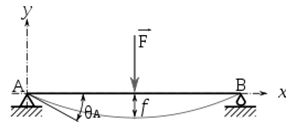
Pour les bâtiments à structure métallique, les planchers, constitués de poutrelles en acier (IPN) ne doivent pas excéder une flèche limite (=déformation)4 - Condition de déformation

En flexion il existe des formulaires de poutres indiquant le Moment de flexion maxi, la flèche maxi et leur position.5 - Formulaire poutres

Exercices
Calculez la contrainte en flexion. La contrainte de flexion σ= (Mf/I).vExercice 1
 Un plancher est soutenu par une poutre IPN.
Un plancher est soutenu par une poutre IPN.
Le moment de flexion maxi, situé au milieu de la poutre, vaut est de 5000 Nm.
La poutre est un IPN 200 de moment d'inertie 2000 cm4
L'IPN est en acier S235 (Re=235 Mpa), on prendra un coefficient de sécurité de 2.
Il ne faut pas oublier de mettre toutes les dimensions en mm
de plus v = demi-hauteur de la poutre = 100mm
σ= [5000.103/(2000.104)].100
σ= 25 Mpa
La poutre est-elle correctement dimensionnée ? La contrainte de flexion maxi est de 50 MPa le matériau de la poutre est un acier S235 et on doit tenir compte d'un coefficient de sécurité de s=2
la résistance "pratique" vaut Re/s = 235/2 = 117,5 MPa.
donc la contrainte (25 MPa) reste inférieure à la résistance de la poutre.
A partir du formulaire (5 - Formulaire poutres), Le cas le plus proche est le 2èmeExercice 2
 Le tablier d'un petit pont est modélisé par la figure ci-contre.
Le tablier d'un petit pont est modélisé par la figure ci-contre.
Ce pont est réalisé avec deux IPN100 parallèles.(Moment d'inertie IPN100 : I=171 cm4).
La charge est de q=250 daN/m.
L'IPN est en acier S235 (Re=235 Mpa), on prendra un coefficient de sécurité de 2.
identifiez le cas (1,2 ou 3) le plus proche de l'énoncé.
Précisez le type de chargement, et d'appuis.
Le chargement est uniformément réparti et il y a 2 appuis simples aux 2 extrémités
Que vaut le moment de flexion maxi, D'après le formulaire le Moment de flexion maxi vaut
et où est-il situé ?
Mf=(2500.42)/8 = 5000 Nm au mileu du pont.
Calculez la contrainte en flexion. La contrainte de flexion σ= (Mf/I).v
Les 2 IPN 100 sont t-ils bien choisi ?
Il ne faut pas oublier de mettre toutes les dimensions en mm et de doubler le moment d'inertie (car le pont possède 2 poutres //).
σ= [5000.103/(2 x 171.104)].50
σ= 146,2 Mpa
La contrainte de flexion maxi est de 146,2 MPa le matériau de la poutre est un acier S235 et on doit tenir compte d'un coefficient de sécurité de s=2
la résistance "pratique" vaut Re/s = 235/2 = 117,5 MPa.
donc la contrainte (146,2 MPa) est supérieure à la résistance de la poutre.
Il faut soit changer la taille des 2 IPN, soit leur matériau.
On change d'IPN pour des IPN 160 (Moment d'inertie 870 cm4), calculez la flèche du pont. D'après le formulaire la fléche a pour expression :
f=(5.p.l4)/(384.E.I)
f=(5.(2500.10-3).(4000)4)/(384.(2.105).(2.870.104))= 2,39 mm au mileu du pont.
Créé avec HelpNDoc Personal Edition: Créer des aides HTML, DOC, PDF et des manuels depuis une même source
